Συνδεθείτε στην Υπηρεσία Νομοσκόπιο Είσοδος στην υπηρεσία Νομοσκόπιο.     Χρήστης Κωδικός   Υπενθύμιση στοιχείων λογαριασμού       Νέοι χρήστες Εάν είστε νέος χρήστης, θα πρέπει να δημιουργήσετε ένα ΔΩΡΕΑΝ λογαριασμό προκειμένου να φύγει το παράθυρο αυτό και να αποκτήσετε πλήρη πρόσβαση στην υπηρεσία Νομοσκόπιο. Δημιουργία νέου λογαριασμού

1. Τύποι Ροής σε Κλειστούς Αγωγούς

 

Οι συνθήκες ροής σε κλειστούς αγωγούς μπορεί να είναι όπως σε ανοικτούς αγωγούς, δηλαδή ροή υπό βαρύτητα και πλήρη αγωγό ή ροή υπό πίεση. Η ροή σε ανοικτούς αγωγούς έχει επιφάνεια νερού εκτεθειμένη στην ατμόσφαιρα, συνθήκη που μπορεί να συμβαίνει και σε κλειστό αγωγό με μερική πληρότητα. Όλες οι αρχές και κανόνες που ισχύουν για τη ροή σε ανοικτούς αγωγούς έχουν εφαρμογή και σε κλειστούς, όταν η ροή γίνεται με μερική πληρότητα. Η ροή με βαρύτητα και με πλήρη αγωγό συμβαίνει όταν ο αγωγός είναι πλήρης αλλά η ροή δε βρίσκεται ακόμη υπό πίεση. Η ροή υπό πίεση συμβαίνει όταν ο αγωγός είναι πλήρης αλλά και υπό πίεση.

 

Επειδή σε ροή κλειστού αγωγού με πληρότητα 100% αλλά υπό συνθήκες βαρύτητας, η βρεχόμενη περίμετρος και η τριβή είναι μεγαλύτερες, η μεταφερόμενη παροχή είναι μικρότερη από εκείνη με πληρότητα του αγωγού < 100%. Για ένα αγωγό κυκλικής διαμέτρου η μέγιστη ροή συμβαίνει όταν το βάθος ροής είναι ίσο με το 93% της διαμέτρου του αγωγού. Η μέση ταχύτητα με βάθος ροής 50% της διαμέτρου του αγωγού είναι ίση με εκείνη της ροής υπό βαρύτητα και πλήρη αγωγό. Η συνθήκη ροής υπό βαρύτητα με πλήρη διατομή συνήθως αποτελεί προϋπόθεση για τους σκοπούς της μελέτης αποχέτευσης ομβρίων. Η εξίσωση Manning συνδυαζόμενη με την εξίσωση συνέχειας σε αγωγό κυκλικής διατομής με πληρότητα 100% μπορεί να γράφεται ως:

 

(6.1-1)

 

όπου:

Q (m3/s): παροχή

n (m-1/3s): συντελεστής Manning

S (m/m): κλίση αγωγού

 

Αυτή η εξίσωση επιτρέπει τον απευθείας υπολογισμό της απαιτούμενης διαμέτρου σωλήνα. Σημειώνεται ότι η υπολογιζόμενη διάμετρος πρέπει να προσαυξάνεται ώστε να λαμβάνεται τουλάχιστον ο αμέσως μεγαλύτερης διαμέτρου σωλήνας από τον Πίνακα 6.1-1 και ώστε το υπολογιζόμενο βάθος ροής ymax για την επιλεγόμενη διάμετρο του σωλήνα, να είναι:

 

 

Πίνακας 6.1-1: Ονομαστικές διάμετροι σωλήνων σκυροδέματος

 

* για μεγαλύτερες διαμέτρους συνήθως ο σωλήνας αντικαθίσταται με ορθογωνική διατομή

 

2. Εξίσωση Ενέργειας

 

Η εξίσωση ενέργειας αναφέρεται στο προηγούμενο κεφάλαιο 3. Με απλά λόγια η εξίσωση δηλώνει ότι το φορτίο ενέργειας σε κάθε διατομή πρέπει να ισούται με εκείνο σε κάθε διατομή στα κατάντη της ροής συν τις ενδιάμεσες απώλειες. Το φορτίο ενέργειας απαρτίζεται από τρεις συνιστώσες: το φορτίο ταχύτητας, το φορτίο πίεσης και το υψόμετρο της στάθμης της επιφάνειας του νερού από το επίπεδο αναφοράς. Η γραμμή ενέργειας αναπαριστά τη συνολική ενέργεια σε κάθε διατομή του αγωγού. Οι απώλειες της ενέργειας ταξινομούνται ως απώλειες τριβής και απώλειες σχήματος (βλέπε επόμενα).

 

Η πιεζομετρική γραμμή υπολείπεται της γραμμής ενέργειας κατά το ποσό του φορτίου ταχύτητας. Σε ροή ανοικτών αγωγών η πιεζομετρική γραμμή ταυτίζεται με τη στάθμη της επιφάνειας του νερού εντός του αγωγού, ενώ σε ροή υπό πίεση η πιεζομετρική γραμμή αντιπροσωπεύει τη στάθμη της επιφάνειας του νερού στην οποία θα φθάσει εντός ενός κατακόρυφου σωλήνα που συνδέεται επί του αγωγού. Για παράδειγμα, σε ένα δίκτυο ομβρίων υπό πίεση η πιεζομετρική γραμμή θα πρέπει να είναι χαμηλότερη από τη στάθμη κυκλοφορίας μιας οδού ή αλλιώς το εντός του δικτύου νερό θα ανέβει από τα στόμια υδροσυλλογής και θα πλημμυρίσει την οδό. Ομοίως, εάν η συνθήκη ροής σε ανοικτό αγωγό είναι υπερκρίσιμη, θα πρέπει να λαμβάνονται μέτρα που θα διασφαλίζουν ότι δε θα συμβαίνει υδραυλικό άλμα, το οποίο μπορεί να δημιουργήσει ροή υπό πίεση, οπότε η πιεζομετρική γραμμή θα ανέβει πάνω από τη στάθμη της οδού.

 

3. Απώλειες Ενέργειας

 

Όταν χρησιμοποιείται η εξίσωση ενέργειας θα πρέπει να συνυπολογίζονται όλες οι απώλειες ενέργειας που ταξινομούνται ως απώλειες τριβής ή απώλειες σχήματος. Οι απώλειες τριβής οφείλονται στις δυνάμεις που αναπτύσσονται μεταξύ του υγρού και των τοιχωμάτων του κλειστού αγωγού, ενώ οι απώλειες σχήματος είναι αποτέλεσμα των ποικίλων υδραυλικών κατασκευών κατά μήκος του κλειστού αγωγού. Αυτές οι κατασκευές, όπως είναι τα φρεάτια επίσκεψης, τα καμπύλα τμήματα του αγωγού, τα τμήματα μεταβατικής διατομής, προκαλούν η καθεμία απώλειες στο φορτίο ταχύτητας και πιθανώς μείζονες αλλαγές στη γραμμή ενέργειας καθώς και στην πιεζομετρική γραμμή κατά μήκος της περιλαμβανόμενης κατασκευής. Αν και οι απώλειες σχήματος συνηθίζεται να αποκαλούνται ελάσσονες απώλειες εντούτοις αυτές μπορεί να είναι σημαντικές σε σύγκριση με τις απώλειες τριβής.

 

3.1. Υπολογισμός απωλειών τριβής

 

Οι απώλειες τριβής υπολογίζονται ως:

 

(6.3.1-1)

 

όπου:

 

L (m): μήκος αγωγού

Sf (m/m): κλίση τριβής (κλίση γραμμής ενέργειας)

 

Τυπικά προϋποτίθεται ότι οι συνθήκες είναι ομοιόμορφης ροής, έτσι η κλίση τριβής μπορεί να υπολογίζεται από, είτε την εξίσωση Manning, είτε την εξίσωση Darcy - Weisbach.

 

Επιλύοντας την εξίσωση Manning ως προς Sf:

 

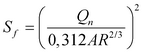(6.3.1-2)

 

Αντιστοίχως η εξίσωση Darcy - Weisbach για ροή σε ανοικτούς αγωγούς είναι:

 

(6.3.1-3)

 

και για ροή υπό πίεση σε κυκλικό αγωγό:

 

(6.3.1-4)

 

Για τον υπολογισμό των απωλειών συνήθως χρησιμοποιείται η εξίσωση Manning, αν και η εξίσωση Darcy - Weisbach θεωρητικά είναι καλύτερη επειδή είναι σωστή από άποψη διαστάσεων και έχει εφαρμογή για κάθε υγρό σε ένα ευρύ φάσμα συνθηκών. Εντούτοις, οι πιθανότητες για μεγαλύτερη ακρίβεια με την εξίσωση Darcy - Weisbach περιορίζονται από τον προσδιορισμό του f και γενικώς τη μεγαλύτερη πολυπλοκότητα της εφαρμογής σε σχέση με την εξίσωση Manning. Οι τυπικές τιμές του συντελεστή τραχύτητας n της εξίσωσης Manning αναφέρονται στον προηγούμενο Πίνακα 4.3.1-1.

 

Ανεξαρτήτως της χρησιμοποιούμενης εξίσωσης, απαιτείται κριτική εκτίμηση στην επιλογή των συντελεστών τραχύτητας n. Ο συντελεστής τραχύτητας κυρίως ορίζεται από το είδος του υλικού του σωλήνα. Εντούτοις, πολλοί άλλοι παράγοντες μπορεί να επιβάλλουν αναπροσαρμογή της τιμής που έχει ορισθεί για ένα συγκεκριμένο υλικό. Τέτοιοι παράγοντες είναι: η ποιότητα των αρμών μεταξύ των σωλήνων, η κακή χάραξη και κλίση του αγωγού που προκαλούν κατακάθιση ή πλευρικές κινήσεις εδαφικού υλικού, αποθέσεις φερτών. Άλλοι παράγοντες είναι η ροή από πλευρικές εισροές που διαταράσσουν την κύρια ροή.

 

3.2. Υπολογισμός απωλειών σχήματος

 

Απώλειες σχήματος συμβαίνουν όταν η ροή διέρχεται από κατασκευές όπως φρεάτια επίσκεψης, συμβολές, καμπύλες, τμήματα μεταβαλλόμενης διατομής. Αυτές οι κατασκευές επιφέρουν σημαντικές απώλειες τόσο στη γραμμή ενέργειας όσο και στην πιεζομετρική γραμμή κατά μήκος του αγωγού, και εάν αυτές δεν υπολογίζονται στο σχεδιασμό, η πραγματική παροχετευτικότητα του αγωγού μπορεί να είναι περιορισμένη.

 

Οι απώλειες σχήματος μπορεί να υπολογίζονται με διάφορες μεθόδους. Η απλούστερη μέθοδος βασίζεται σε ένα συντελεστή πολλαπλάσιο του φορτίου ταχύτητας. Αυτός ο συντελεστής λαμβάνει διάφορες τιμές αντιστοίχως με το είδος της κατασκευής που δημιουργεί τις απώλειες, φρεάτια επίσκεψης, καμπύλες, στόμια υδροσυλλογής, κ.τ.λ.). Η γενική μορφή της εξίσωσης είναι:

 

(6.3.2-1)

 

Μια εναλλακτική μέθοδος βασίζεται στο άθροισμα των τεσσάρων μεμονωμένων απωλειών που ορίζονται ως συνάρτηση της ταχύτητας: απώλειες εισόδου / εξόδου, απώλεια διόρθωσης ταχύτητας, απώλεια καμπύλης και απώλεια συμβολής. Ίσως η πλέον εξεζητημένη προσέγγιση βασίζεται σε παραδοχές που έχουν σχέση με την πίεση και την ορμή, ειδικότερα στο ότι το άθροισμα όλων των πιέσεων που επενεργούν σε μια συμβολή πρέπει να είναι ίσο με το άθροισμα όλων των ορμών.

 

3.2.1. Απώλειες λόγω παρεμβολής φρεατίων επίσκεψης

 

Ειδικά λογισμικά όπως τα Δίκτυα Ύδρευσης της TechnoLogismiki χρησιμοποιούν διάφορες μεθόδους για τον υπολογισμό των απωλειών σχήματος π.χ. οι απώλειες σε φρεάτιο επίσκεψης υπολογίζονται ως ένας συντελεστής που είναι πολλαπλάσιος του φορτίου ταχύτητας. Ο συντελεστής Κ έχει προσδιορισθεί πειραματικά ως:

 

(6.3.2.1-1)

όπου:

 

K: ο προσαρμοσμένος συντελεστής απώλειας φορτίου

Κ0: ο συντελεστής αρχικής απώλειας φορτίου με βάση το σχετικό μέγεθος του φρεατίου επίσκεψης

CD: ο συντελεστής διόρθωσης λόγω αλλαγής διαμέτρου σωλήνα

Cd: ο συντελεστής διόρθωσης λόγω βάθους ροής

CQ: ο συντελεστής διόρθωσης λόγω συμβολής πλευρικής ροής

Cp: ο συντελεστής διόρθωσης λόγω υψομετρικής πτώσης της ροής

CB: ο συντελεστής διόρθωσης λόγω καμπύλης

 

Ο συντελεστής αρχικής απώλειας φορτίου Κ0 υπολογίζεται ως συνάρτηση του σχετικού μεγέθους του φρεατίου και της γωνίας μεταξύ των σωλήνων εισροής και εκροής.

 

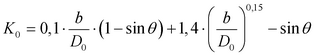(6.3.2.1-2)

 

όπου:

 

Κ0: ο συντελεστής αρχικής απώλειας φορτίου βασιζόμενος στο σχετικό μέγεθος του φρεατίου επίσκεψης

θ: η γωνία που σχηματίζουν μεταξύ τους οι δυο σωλήνες εισροής και εκροής

b: η διάμετρος του φρεατίου

D0: η διάμετρος του σωλήνα εκροής

 

Έχει αποδειχθεί ότι υπάρχουν μόνο μικρές διαφορές στο συντελεστή απώλειας φορτίου μεταξύ φρεατίων κυκλικής και ορθογωνικής διατομής. Ως εκ τούτου το σχήμα του φρεατίου μπορεί να αγνοείται όταν υπολογίζονται οι απώλειες φορτίου για τους σκοπούς της μελέτης.

 

Ο συντελεστής διόρθωσης λόγω αλλαγής διαμέτρου σωλήνα μεταξύ δυο διαδοχικών σωλήνων υπολογίζεται ως:

 

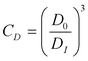(6.3.2.1-3)

 

όπου:

 

CD: ο συντελεστής διόρθωσης λόγω αλλαγής διαμέτρου σωλήνα

DI: η διάμετρος του προσαγωγού σωλήνα

D0: η διάμετρος του απαγωγού σωλήνα

 

Μια αλλαγή στην απώλεια φορτίου λόγω διαφορών στις διαμέτρους των σωλήνων έχει αποδειχθεί ότι είναι σημαντική μόνο υπό συνθήκες πίεσης, όταν ο λόγος του βάθους του νερού στο φρεάτιο επίσκεψης προς τη διάμετρο του απαγωγού σωλήνα, είναι d/D0>3,2. Ως εκ τούτου γίνεται εφαρμογή μόνο σε τέτοιες περιπτώσεις.

 

Ο συντελεστής διόρθωσης λόγω βάθους ροής, Cd, υπολογίζεται ως:

 

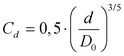(6.3.2.1-4)

όπου:

 

Cd: ο συντελεστής διόρθωσης λόγω βάθους ροής

d: το βάθος νερού στο φρεάτιο επίσκεψης πάνω από τη στέψη του απαγωγού σωλήνα

D0: η διάμετρος του απαγωγού σωλήνα

 

Αυτός ο συντελεστής διόρθωσης έχει βρεθεί ότι είναι σημαντικός μόνο στις περιπτώσεις ροής με ελεύθερη επιφάνεια ή υπό μικρή πίεση, όταν ο λόγος d/D0<3,2, και εφαρμόζεται μόνο σε τέτοιες περιπτώσεις. Το βάθος νερού στο φρεάτιο επίσκεψης προσομοιάζεται με τη στάθμη της πιεζομετρικής γραμμής στο ανάντη άκρο του απαγωγού σωλήνα.

 

Ο συντελεστής διόρθωσης λόγω συμβολής πλευρικής ροής, CQ, υπολογίζεται ως:

 

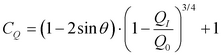(6.3.2.1-5)

όπου:

 

C0: ο συντελεστής διόρθωσης λόγω συμβολής πλευρικής ροής

θ: η γωνία που σχηματίζουν μεταξύ τους οι δυο σωλήνες εισροής και εκροής

QI: η ποσότητα ροής στον προσαγωγό σωλήνα

Q0: η ποσότητα ροής στον απαγωγό σωλήνα

 

Ο συντελεστής CQ είναι μια συνάρτηση της γωνίας της προσερχόμενης ροής όπως επίσης του ποσοστού της προσερχόμενης ροής δια του σωλήνα που ενδιαφέρει και αντιστρόφως ανάλογος της ροής των άλλων προσερχόμενων σωλήνων. Το γεγονός αυτό καταδεικνύεται με τη βοήθεια του σχήματος 6.3.2.1-1 όπου δίνονται οι παραδοχές: Q1 = 3 m3/s, Q2 = 1 m3/s και Q3 = 4 m3/s. Επιλύοντας το συντελεστή διόρθωσης για τη σχετική ροή κατά την πορεία από το σωλήνα #3 προς ένα από τους προσερχόμενους σωλήνες π.χ. το σωλήνα #2:

 

 

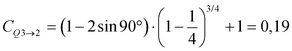(6.3.2.1-6)

 

Για ένα δεύτερο παράδειγμα με τις παραδοχές: Q1 = 1 m3/s, Q2 = 3 m3/s και Q3 = 4 m3/s. Υπολογίζοντας το συντελεστή Q0 σε αυτή την περίπτωση είναι:

 

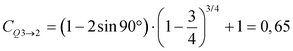(6.3.2.1-7)

 

Και στις δυο περιπτώσεις η προσερχόμενη ροή δια του σωλήνα #2 έχει να κάνει πορεία με γωνία 90° για να πάει στο σωλήνα #3. Στην περίπτωση 1 η μεγαλύτερη ροή διανύει ευθύγραμμη πορεία μέσα από το φρεάτιο, από το σωλήνα #1 προς το σωλήνα #3, υποβοηθώντας τη ροή από το σωλήνα #2 για να κάνει τη στροφή. Στην περίπτωση 2, η κύρια ροή προσέρχεται δια του σωλήνα #2. Η υποβοήθηση από την ευθύγραμμη διερχόμενη ροή, της ροής του σωλήνα #2 προς το σωλήνα #3, είναι μικρότερη. Ως αποτέλεσμα το συντελεστής διόρθωσης για τη σχετική ροή στην περίπτωση 1 έχει τιμή 0,19 δηλαδή είναι πολύ μικρότερος από το συντελεστή διόρθωσης της περίπτωσης 2 όπου αυτός έχει τιμή 0,65.

 

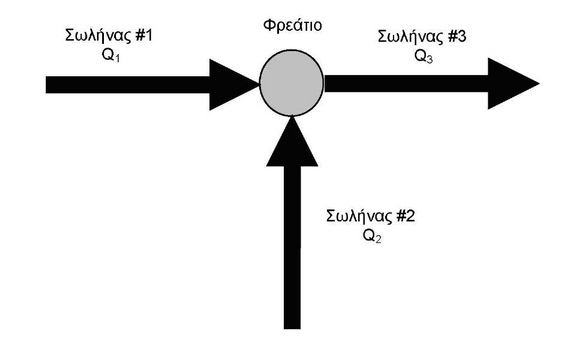
Σχήμα 6.3.2.1-1: Παράδειγμα συμβολής ροής

 

Ο συντελεστής διόρθωσης λόγω υψομετρικής πτώσης της ροής, CP, υπολογίζεται ως:

 

(6.3.2.1-8)

 

όπου:

CP: ο συντελεστής διόρθωσης λόγω υψομετρικής πτώσης της ροής

h: το κατακόρυφο ύψος της πτώσης της ροής από τη στέψη του προσαγωγού σωλήνα μέχρι το κέντρο του απαγωγού σωλήνα

D0: η διάμετρος του απαγωγού σωλήνα

d: το βάθος νερού εντός του φρεατίου

 

Αυτός ο συντελεστής διόρθωσης αντιστοιχεί με την επιρροή της συμβολής πλευρικού σωλήνα, που πέφτει μέσα στο φρεάτιο, επί της ροής του προσαγωγού σωλήνα για την οποία γίνεται ο υπολογισμός της απώλειας φορτίου. Χρησιμοποιώντας τους συμβολισμούς του προηγούμενου σχήματος, για παράδειγμα ο συντελεστής CP υπολογίζεται για το σωλήνα #2, όταν ο σωλήνας #1 παροχετεύει ροή με πτώση. Η ροή που προκύπτει από την πτώση και προέρχεται από την προσαγόμενη ροή διαμέσου της οπής επί του φρεατίου, λαμβάνεται υπόψη κατά τον ίδιο τρόπο. Ο συντελεστής διόρθωσης εφαρμόζεται μόνο όταν h>d.

 

Ο τελικός συντελεστής διόρθωσης πολλαπλασιαζόμενος επί το συντελεστή K0 προκειμένου να γίνει η διόρθωση του συντελεστή απώλειας φορτίου K είναι η διόρθωση CB, λόγω καμπύλης μέσα στο φρεάτιο. Η καμπύλη κατασκευή εντός του φρεατίου έχει σκοπό να κατευθύνει τις ροές μέσα από το φρεάτιο, με αποτέλεσμα την ελάττωση των απωλειών φορτίου. Οι συντελεστές διόρθωσης λόγω καμπύλης, CB, παρουσιάζονται στον επόμενο Πίνακα 6.3.2.1-1.

 

Πίνακας 6.3.2.1-1: Συντελεστές διόρθωσης, CB, λόγω καμπύλης

 

3.2.2. Απώλειες λόγω μεταβαλλόμενης διατομής

 

Αυτή υπολογίζεται ως:

 

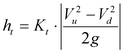(6.3.2.2-1)

όπου:

 

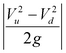: η απόλυτη τιμή της διαφοράς του φορτίου ταχύτητας μεταξύ ανάντη και κατάντη

Kt: λαμβάνεται 0,1 για αυξανόμενη και 0,2 για ελαττούμενη ταχύτητα

 

Για ροή υπό πίεση που διέρχεται από τμήμα μεταβαλλόμενης διατομής εφαρμόζεται η εξίσωση:

 

Μεταβολή αυξανόμενης διατομής

 

 

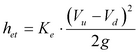(6.3.2.2-2)

όπου:

 

Ke: λαμβάνεται 1,0 για απότομη αύξηση διατομής

Ke: λαμβάνεται 0,2 στην περίπτωση σχεδιασμένης μεταβολής

 

3.2.3. Απώλειες λόγω καμπύλης

 

Μετρήσιμη απώλεια λόγω καμπύλης συμβαίνει όταν ένας αγωγός παρουσιάζει αλλαγή κατεύθυνσης >15°. Ο υπολογισμός αυτής της απώλειας εκφράζεται ως:

 

(6.3.2.3-1)

 

όπου:

 

V: η ταχύτητα ροής μέσα στο σωλήνα

Kb:

φ: η επίκεντρη γωνία της καμπύλης σε μοίρες